遞迴 - Recursion

疊代 (iterative)

用迴圈去循環重複程式碼的某些部分來得到答案，而遞迴法(recursive method)則是重複呼叫自身程式碼來得到答案。

遞迴 (recursive)

找出問題的規律，以此規律重複用相同手法來縮減問題範圍，直到能釐清細節，找到確定的部份。

遞迴的定義：一個函數定義中，直接引用函數的本身，則此函數就稱為遞迴函數（recursive function）。

遞迴（Recursion），是指在函式中使用函式自身的方法。
遞迴函式必須有終止條件，才能被計算。

以 n! (階層函式) 為例子來了解遞迴

階層函式解說影片(英文)

舉例來說 4! = 4 x 3 x 2 x 1 = 24，接著讓我們來看看疊代與遞迴的程式

疊代版本

int factorial(int n)
{
    int i=0, ans=1;
    if(n<=0) return 1;
    for(i=1; i<=n; ++i) ans*=i;
    return ans;
}

遞迴版本

int factorial_rec(int n) 
{
    if(n==1)
        return 1;
    else
        return n*factorial_rec(n-1);
}

跟著下圖流程一起走過一遍，就能了解遞迴的原理了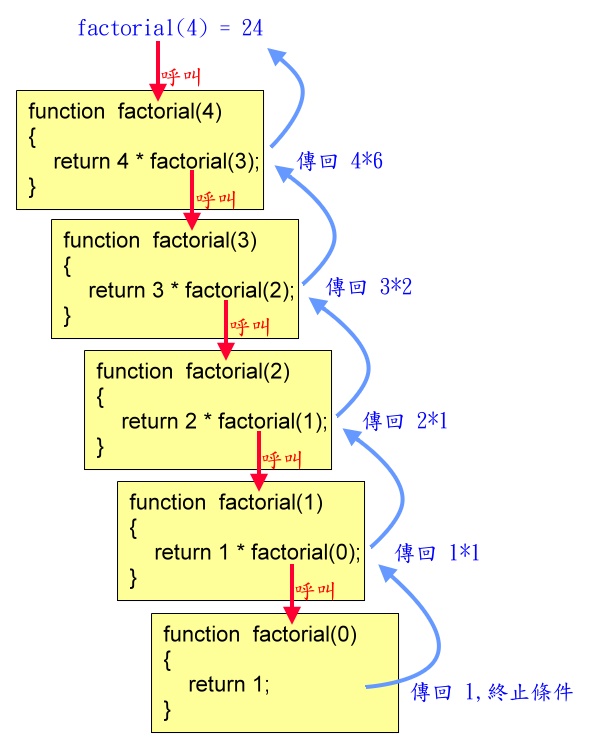

次方 - f(a,b) 代表a的b次方計算結果

#include<iostream>
using namespace std;

int f(int a, int b)
{
    if( b == 0 )
        return 1;
    if( b >= 1 )
        return a * f(a,b-1);
}

int main()
{
    int a, b;
    while( cin >> a >> b )
    {
        cout << f(a,b) << endl;
    }

    return 0;

小技巧 : 快速次方 a^b Time Complexity : $$log(b)$$

#include<iostream>
using namespace std;

int f(int a, int b)
{
    if( b == 0 )
        return 1;
    if( b % 2 == 0 ){
        int x = f( a , b/2 );
        return x * x;
    }
    else
        return a * f(a,b-1);
}

int main()
{
    int a, b;
    while( cin >> a >> b )
    {
        cout << f(a,b) << endl;
    }

    return 0;
}

接著練習一下這兩題

1-2+3-4+5-6+7-8+...+n

哪些數字是負數，那些是正數，找出規律

輸入

5   ← 1-2+3-4+5 = 3
10
20

輸出

3
-5
-10

1+4+9+16+25+36+49+81+......

輸入

3   ← 1+4+9 = 14
10
20

輸出

14
385
2870

參考資料：

課程要點：

先介紹一下疊代，接著簡介遞迴的定義
以n!為例，照圖講解整個遞迴流程
讓學生做幾個簡單的練習：1-2+3-4...與1+4+...+n^2
對遞迴有感，接著講解Divide and Conquer章節，了解遞迴更深一步的應用，像是Binary Search。
經典範例講解：河內塔...
留時間讓學生做課堂練習

4.Recursion