APCS
詳細解答
1.
int A[8]={0, 2, 4, 6, 8, 10, 12, 14};
int Search (int x) {
int high = 7;
int low = 0;
while (high > low) {
int mid = (high + low)/2;
if (A[mid] <= x) {
low = mid + 1;
} else {
high = mid;
}
}
return A[high];
}
Search(x) 真正目的是找到 A 之中大於 x 的最小值,Search(16)會回傳14。
2.
F(n)本身會輸出n個星星,如果n>1就去然後再去call兩個F(n/2),由小算到大
選項A A1(5) → F(1) F(4) A2(5) → F(2) F(3)
選項B A1(13) → F(2) F(10) A2(13) → F(5) F(7)
選項C A1(14) → F(2) F(11) A2(14) → F(5) F(8)
選項D A1(15) → F(3) F(12) A2(15) → F(6) F(9)
先算出數字F(2),接著算F(3), F(4)等 這樣F(8)->F(4)F(4)就能直接帶入已算出結果的F(4)答案
3.
int F (int n) {
if (n < 4)
return n;
else
return _______?_______;
}
(A) n * F(n-1) → 14 x 13 x 12 x ... x 3 (B) n + F(n-3) → 14 + 11 + 8 + 5 + 2 = 40 (C) n - F(n-2) → `14 - 12 - 10 - ... - 2 (D) F(3n+1) → 越變越大,無法收斂
4.
- a是被除數,b是除數,r是餘數
- 當r=0也就是除盡,除數就是最大公因數,也就是b
- GCD(b,r),因為輾轉相除舊式被除數與除數互換,所以a跟b應該要互換位置,然後a被b除後剩下r,
5.
q可能等於p
6.
rowsum沒有歸零
7.
輸出base case的次數代表遇到終止條件的次數,可以畫遞迴的樹狀圖,下圖來看就是綠色的總數目,而橘色代表的是已經有代入同樣參數的function算出結果,藍色虛線告訴你是哪個function已算出結果。
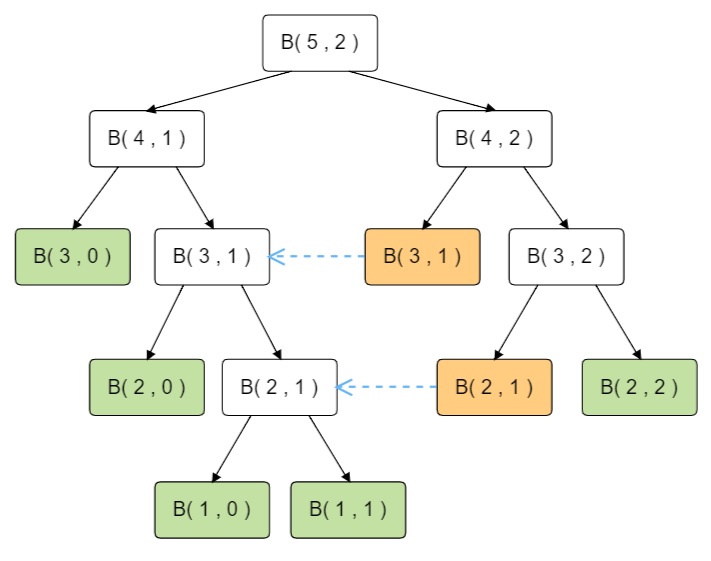
8.
考全域變數概念,代入就可以算出答案,簡單的題目
9.
void F () {
int X[10] = {0};
for (int i=0; i<10; i=i+1) {
scanf("%d", &X[(i+2)%10]);
}
}
依序輸入順序為
| 對應的X[] (計算前) | 對應的X[] | i |
|---|---|---|
| X[(0+2)%10] | X[2] | 0 |
| X[(1+2)%10] | X[3] | 1 |
| X[(2+2)%10] | X[4] | 2 |
| X[(3+2)%10] | X[5] | 3 |
| X[(4+2)%10] | X[6] | 4 |
| X[(5+2)%10] | X[7] | 5 |
| X[(6+2)%10] | X[8] | 6 |
| X[(7+2)%10] | X[9] | 7 |
| X[(8+2)%10] | X[0] | 8 |
| X[(9+2)%10] | X[1] | 9 |
提示:
中間的區域找出規律就不需要一個一個代入,只需要注意
X[(8+2)%10]之後就可以了。
10.
int n = 0;
void K (int b) {
n = n + 1;
if (b % 4)
K(b+1);
}
void G (int m) {
for (int i=0; i<m; i=i+1) {
K(i);
}
}
- n 代表的是K()一共被執行幾次
- G(100)會執行 K(0) K(1) K(2) ... K(98) K(99),第一波K()會被執行100次
- K(n) 如果n不是4的倍數的話,就會遞迴
- 0~99中是4倍數有幾個,一共100/4 = 25個K()會停止執行遞迴,代表還剩75個數字會進行遞迴
- 接著會再做 75, 50, 25 次
- 所以100+75+50+25 = 250
11.
swap概念
12.
- rand() % 900 算出的結果為 0 ~ 899
- rand() % 901 算出的結果為 0 ~ 900
- rand() % 901 + 100 算出的結果為 0+100 ~ 900+100,意即 100~1000
13.
for (int i=0; i<=100; i=i+5) {
printf ("%s\n", "Hi!");
}
以上程式碼會執行21次,如果一時看不出來可以先把程式改成
for (int i=0; i<=5; i=i+5) {
printf ("%s\n", "Hi!");
}
這樣會執行2次,分別在i=0以及i=5時輸出Hi
14.
這題在問總共會被F()會執行幾次,稍微觀察過程式後,會發現數字如果為不大於1的奇數時會終止條件,這題目前看來只能硬算
輸出結果
F(15) 15
F(5n+1) 76
F(n/2) 38
F(n/2) 19
F(5n+1) 96
F(n/2) 48
F(n/2) 24
F(n/2) 12
F(n/2) 6
F(n/2) 3
F(5n+1) 16
F(n/2) 8
F(n/2) 4
F(n/2) 2
F(n/2) 1
15.
void F (int a) {
while (a < 10)
a = a + 5;
if (a < 12)
a = a + 2;
if (a <= 11)
a = 5;
}
提示:
(A) a只要輸入任一個<10的數字即可執行a=a+5 (B) 因為a<10就會被+5,所以a=11符合條件,或是11-5n,n為正整數,也符合條件 (C)a<10的狀況都會被+5最後就會超過11,而a=11的狀況也會因為if (a < 12)的狀況讓a變成13,所以a = 5;永遠執行不到
16.
代入參數後,發現這個判斷式當a=7時回傳true,a=8則回傳false,接著就用這個前提去測試每個選項。
17
int F (int n) {
int x = 0;
for (int i=1; i<=n; i=i+1)
for (int j=i; j<=n; j=j+1)
for (int k=1; k<=n; k=k*2)
x = x + 1;
return x;
}
前面的
for (int i=1; i<=n; i=i+1)
for (int j=i; j<=n; j=j+1)
可以用梯形公式來看,如果我們把它改寫成印出星星的程式
for (int i=1; i<=n; i=i+1){
for (int j=i; j<=n; j=j+1){
cout<<"*";
}
cout<<endl;
}
那們印出星星的總數量就相當於時間複雜度 如果n=3,則會輸出下圖
***
**
*
我們要用梯形弓是(上底+下底)高/2,也就是(1+n)n/2,最後整理成公式 n(n+1)/2,也就是時間複雜度。
而for (int k=1; k<=n; k=k*2),這行則寫成⌊log2n + 1⌋,⌊⌋符號表示floor(),也就是取小於此數的最大整數,⌊3.6⌋=3,看下表就能了解為何要寫成這樣了
| n | 執行次數 | ⌊log2n⌋ | ⌊log2n + 1⌋ |
|---|---|---|---|
| n=1 | 1 | 0 | 1 |
| n=2 | 2 | 1 | 2 |
| n=3 | 2 | 1 | 2 |
| n=4 | 3 | 2 | 3 |
18.
i與j相加的關係圖,聰明的你如果會畫這張圖,就不用一個一個代入參數去計算了,雖然這張圖畫出來也等同於全部算出來。
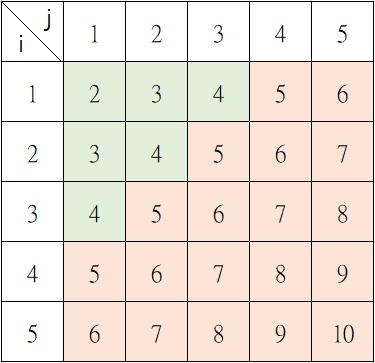
19.
這題的M是最大值,N是最小值,但這程式的瑕疵是不該用if-else,應該個用一個if才對
解答b會找出bug的原因是因為每次碰到判斷式都剛好執行if then的部分,所以else執行不半次而測出問題
20.
這題一個重要的觀念是scope
int g1 = 30, g2 = 20;
int f1(int v) {
int g1 = 10;
return g1+v;
}
int f2(int v) {
int c = g2;
v = v+c+g1;
g1 = 10;
c = 40;
return v;
}
int main() {
g2 = 0;
g2 = f1(g2);
printf("%d", f2(f2(g2)));
return 0;
}
提示:
- 程式執行是一步一步來,所以先看main()
- main()中的g2=0會去修改全域變數g2
g2 = f1(g2);為g2 = f1(0);f(0)回傳 10,因為int g1 = 10;是區域變數,不會用到全域變數int g1 = 30- 執行
f2(f2(10)),f2中的g1跟g2都是全域變數,首先先執行內部的f2(10),回傳50,c = 40;只在function中有用,所以function結束後c就會消失,這題的c是陷阱。而全域變數的g1從30被改成10 - f2(f2(10))現在變成了f2(50),而此時的全域變數g1=10, g2=10,答案為70
21.
遞迴題目
int F (int x,int y) {
if (x<1)
return 1;
else
return F(x-y,y)+F(x-2*y,y);
}
計算過程:
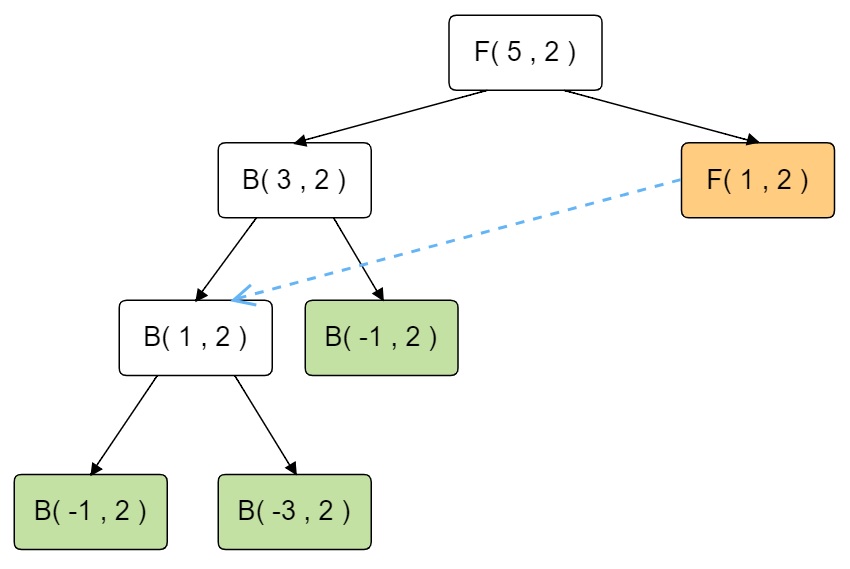
提示:
F(1,2) 在題目中會重複出現,所以可以如果已經算出F(1,2)的結果,那碰到第二個F(1,2)就不需要重算了
22.
!(X1 || X2) = True X1 || X2 = False
25.
(D) 應該也是對的