DFS vs BFS ( 深度優先搜尋法 vs 廣度優先搜尋法 )

Graph 與 Tree

在學DFS與BFS前，應該先了解Graph與Tree這些概念，所以我們先來看看以下的教材。

實作Tree的練習

一開始先輸入一個數字N，代表Tree的節點數量，N不超過7 接下來有N行資料，N行中的第1行代表node 0的parent是誰，N行中的第2行代表node 1的parent是誰，以此類推，如果是該節點是root，那parent為-1。

最後請輸出，所有葉節點，並且算出葉節點與根節點的距離

輸入

4  <- 4個節點
-1 <- 0的parent是-1，代表0是root
0  <- 1的parent是0
1  <- 2的parent是1
0  <- 3的parent是0

3
2
-1
1

5
-1
0
1
1
2

輸出

葉節點[2]與根節點距離差2
葉節點[3]與根節點距離差1

葉節點[0]與根節點距離差2

葉節點[3]與根節點距離差2
葉節點[4]與根節點距離差3

程式碼

#include <bits/stdc++.h>
using namespace std;

int main()
{
    //最多7個node
    bool leaf[7]; //是葉節點的話為true
    int parent[7]; // 記錄每個節點的parent，root的話，parent填-1
    int nodeCount; // 這棵Tree有幾個node

    cin>>nodeCount;
    for(int i=0;i<nodeCount;i++){
        leaf[i]=true;
    }

    //判斷哪些節點是葉節點(leaf)
    for(int i =0;i<nodeCount;i++){
        cin>>parent[i];
        if(parent[i]>=0){
            leaf[parent[i]]=false;
        }else{
            // 遇到根節點的特殊處理
            leaf[i]=false;
        }
    }

    //找出所有的葉節點(leaf)，並且輸出該葉節點與根節點(root)的距離
    for(int i =0;i<nodeCount;i++){
        if(leaf[i]==true){
            int height=0;
            int idx=i;
            while(parent[idx]>=0){
                height++;
                idx=parent[idx];
            }
            cout<<"葉節點["<<i<<"]與根節點距離差"<<height<<endl;
        }

    }
}

DFS ( 深度優先搜尋法)

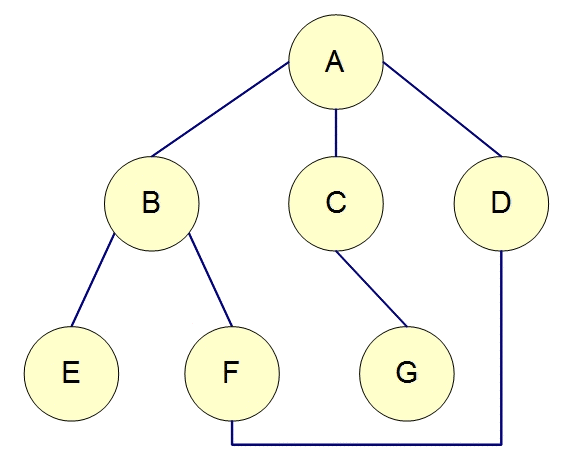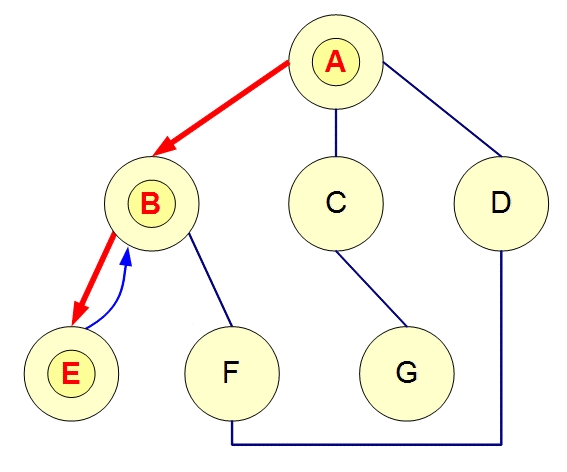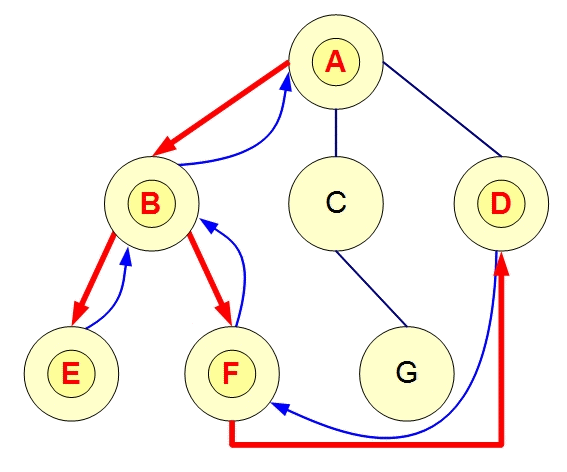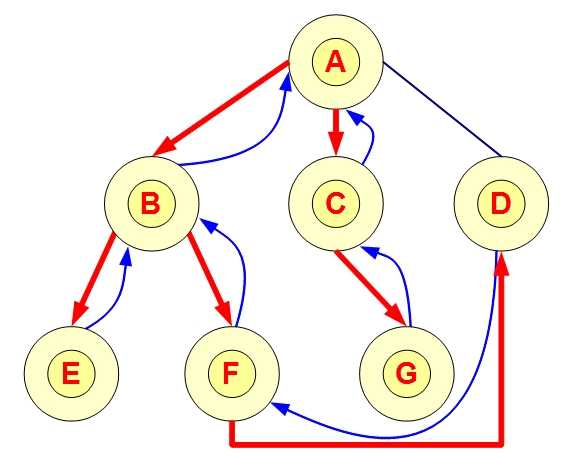
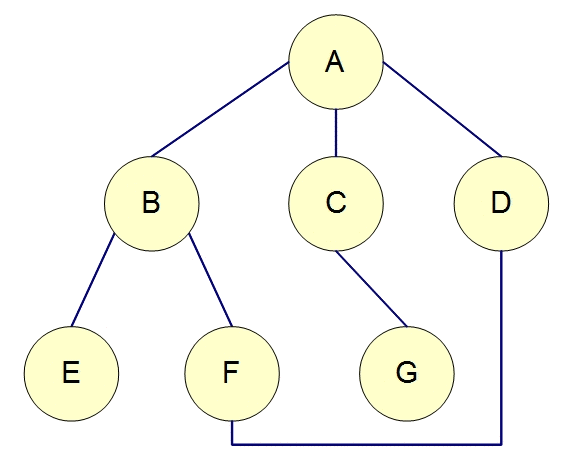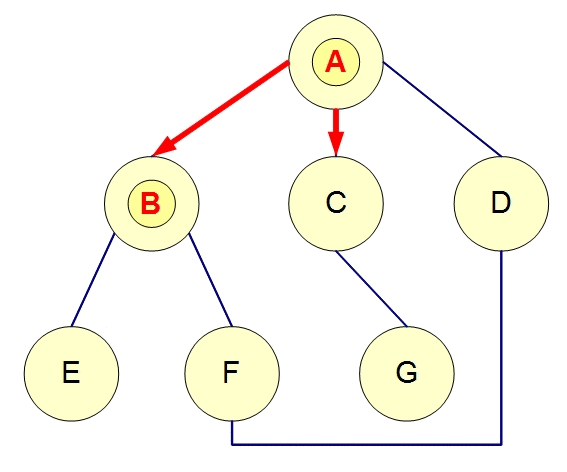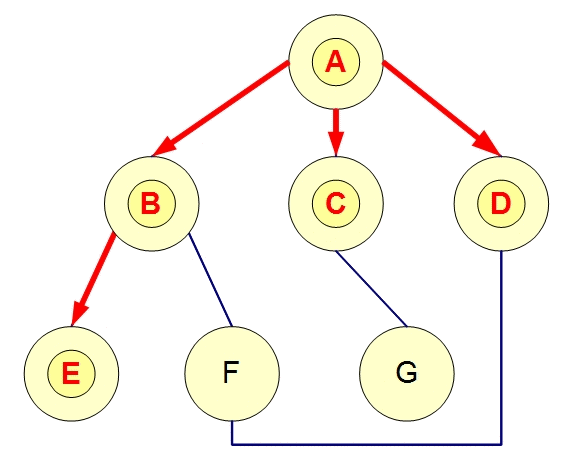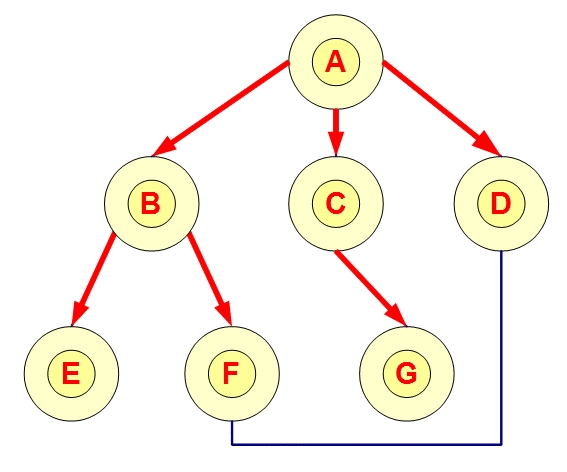
想像很多寶物藏在下圖的某些點中，連線代表道路，我們需要找遍全部的點才能找完寶物。
若從A點開始尋找寶物，我們搜尋寶物的過程會是如何?

[輸出拜訪順序] 若從A開始走，走過的不用再走。

來試試看DFS 模擬程式1號 與 模擬程式2號

DFS
搜尋順序 : A, B, E, F, D, C, G

下圖是使用DFS來搜尋迷空的唯一出口

DFS 遊走範例 ：

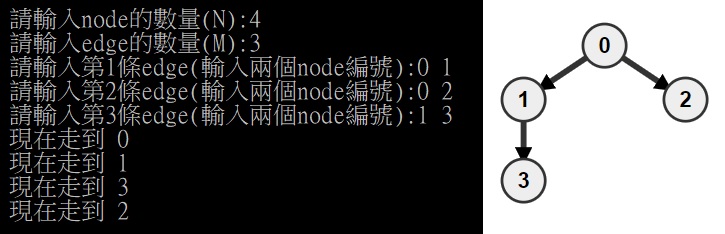
#include <iostream>
#include <algorithm>
using namespace std;
bool edge[105][105],
visited[105];
int N, M;

void DFS( int u ){
    // 代表我現在人在 u
    cout << "現在走到 " << u << endl;

    visited[u] = true;
    for ( int v = 0 ; v < N ; v++ )
        if ( edge[u][v] ){
            // edge[u][v] 代表 u<-->v
            // u有一條邊走到v
            if ( !visited[v] ){
                DFS( v );
                // 走 v
            }
        }
}

int main(){

    int x, y;

    // 假設 Ｎ個點 Ｍ條邊
    cout<<"請輸入node的數量(N):";
    cin >> N;

    cout<<"請輸入edge的數量(M):";
    cin >> M;

    // 初始化邊， 一開始都沒有任何邊
    for ( int i = 0 ; i < N ; i++ )
        for ( int j = 0 ; j < N ; j++ )
            edge[i][j] = false;

    // 一開始所有點都還沒有走過
    for ( int i = 0 ; i < N ; i++ )
        visited[i] = false;

    // 現在輸入 Ｍ 條邊， 每條邊  x <--> y
    for ( int i = 0 ; i < M ; i++ ){
        cout<<"請輸入第"<<(i+1)<<"條edge(輸入兩個node編號):";
        cin >> x >> y;
        edge[x][y] = true;
        edge[y][x] = true;
    }

    //從 0 開始走
    DFS( 0 );

    return 0;
}

BFS ( 廣度優先搜尋法 )

來試試看BFS 模擬程式1號 與 模擬程式2號

BFS
搜尋順序 : A, B, C, D, E, F, G

BFS執行起來的樣子如下，可以用來搜尋迷宮中離自己最近的出口

BFS遊走範例：

#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
bool edge[105][105];
bool visited[105], dist[105];
queue< int > Q;
int N, M;


int main(){
    int x, y;

    // 假設 Ｎ個點 Ｍ條邊
    cout<<"請輸入node的數量(N):";
    cin >> N;

    cout<<"請輸入edge的數量(M):";
    cin >> M;

    // 初始化邊， 一開始都沒有任何邊
    for ( int i = 0 ; i < N ; i++ )
        for ( int j = 0 ; j < N ; j++ )
            edge[i][j] = false;

    // 一開始所有點都還沒有走過
    for ( int i = 0 ; i < N ; i++ )
        visited[i] = false;

    // 現在輸入 Ｍ 條邊， 每條邊  x <--> y
    for ( int i = 0 ; i < M ; i++ ){
        cout<<"請輸入第"<<(i+1)<<"條edge(輸入兩個node編號):";
        cin >> x >> y;
        edge[x][y] = true; // x節點到y節點的邊相連 
        edge[y][x] = true; // y節點到x節點的邊相連 
    }

    // 從節點0開始搜尋
    dist[0] = 0; // 所以Node 0的距離為0
    visited[0] = true; // Node 0被造訪了，因為他是起點
    Q.push( 0 );

    while ( !Q.empty() ){
        int u = Q.front();
        Q.pop();

        cout << "現在走到 " << u << ", 距離是 " << dist[u] << endl;

        // 檢查節點u旁與所有節點的關係
        for ( int v = 0 ; v < N ; v++ ){
            // 如果u跟v之間有連線 且 節點v還沒被造訪過 則代表他是下一層該造訪的節點
            if ( edge[u][v] && !visited[v] ){
                dist[v] = dist[u] + 1;
                Q.push( v );
                visited[v] = true;
            }

        }
    }
    return 0;
}

比較DFS與BFS

DFS BFS
A, B, E, F, D, C, G A, B, C, D, E, F, G

比喻

DFS像

  • 玩RPG(神奇寶貝、仙劍奇俠傳、Final Fantasy、空之軌跡)，控制一個角色走迷宮
  • 翻培訓講義，裡面有連結連到別的講義，裡面又有連結連到別的講義....

BFS像

  • 玩星海爭霸，蟲族擴張領地
  • 拿一杯水倒在紙上，往四周暈開

問題處理類型

DFS可以解決

  • 從某一點出發，總共能走過那些點?
  • 能不能從迷宮的入口走到出口?
  • 一筆畫能不能畫完某張圖?
  • 窮舉所有可能，硬爆問題
  • ...

BFS可以解決

  • 從某一點出發，總共能走過那些點?
  • 能不能從迷宮的入口走到出口?
  • 從A點到B點最短路徑多長?
  • 做什麼事最少需要幾步?
  • ...

延伸閱讀：

Dijkstra's algorithm (戴克斯特拉演算法)：

  • Dijkstra's algorithm其實就是BFS，只是每個edge的權重可能不只1。

A* algorithm (A-Star 演算法)：

  • 遊戲中最常用到的尋找路徑演算法，可以看看影片

參考資料：

results matching ""

    No results matching ""